The Integral Calculator supports definite and indefinite integrals (antiderivatives) as well as integrating functions with many variables You can also check your answers!Integral of e^ {x^2} \square!Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!

Ex 7 5 6 Integrate 1 X2 X 1 2x Class 12 Ex 7 5
Integral dupla de e^(x^2+y^2)
Integral dupla de e^(x^2+y^2)- Homework Statement We define the improper integral (over the entire plane R^2) I as a double integral inf,infx inf,inf of e^ (x^2y^2)dA as equal to the lim as a> inf of the double integral under Da of e^ (x^2y^2)dA where Da is the disk with the radius a and center at the origin Show that the I (the original double integral) equals piMethod 2 Integrate first with respect to y and then x, ie draw a vertical line across D at a typical x value Such a line enters D at y = x 2 and leaves at y = 2x




Gaussian Integral Wikipedia Republished Wiki 2
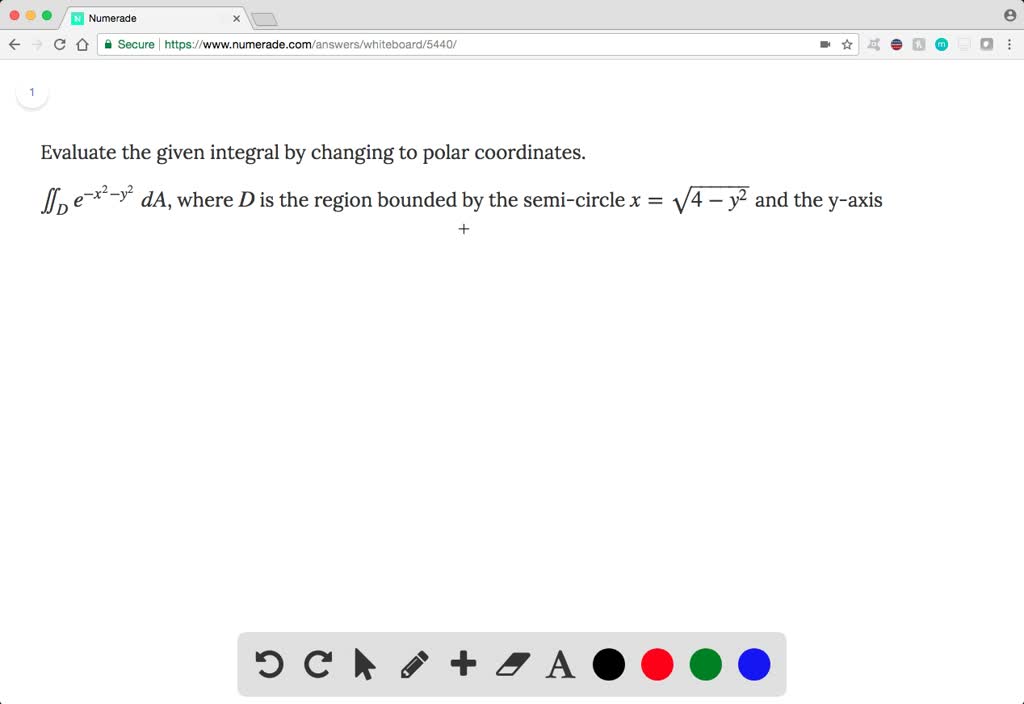
Polar Coordinates Evaluate the integral ZZ D e x2 y2 dA, where Dis the region bounded by the semicircle x= p 4 y2 and the yaxis ZZ D e x2 y2 dA= Z 2 r=0 Z ˇ=2 = ˇ=2 er2rdrd = ˇ Z 2 r=0 rer2 dr ˇ 2 er2j2 0 = ˇ 2 (e4 1) Find the volume of the solid inside the sphere x 2 y2 z = 16 and outside the cylinder x2 y2 = 4 Express this as twice the integral of the function z=Find the value of the integral ∫ 1 0∫ 1 0e max ( x 2, y 2) dxdy I am currently having difficulty trying to evaluate a certain double integral then ∫1 0∫1 0e max ( x2, y2) dxdy = ∫1 0ex2dx since the inner integral does not depend on y I believe that this is correct It is at this point that I cannot evaluate θ y = r sin θ r 2 = x 2 y 2 We are now ready to write down a formula for the double integral in terms of polar coordinates ∬ D f (x,y) dA= ∫ β α ∫ h2(θ) h1(θ) f (rcosθ,rsinθ) rdrdθ ∬ D f ( x, y) d A = ∫ α β ∫ h 1 ( θ) h 2 ( θ) f ( r cos
) r 0 and 0 ˇ=2g Writing x2 y2 as r2 and dxdyas rdrd , J2 = Z ˇ=2 0 Z 1 0 e 2r rdrd = Z 1 0 re r2 dr Z ˇ=2 0 d = 1 2 e 2r 1 0 ˇ 2 = 1 2 ˇ 2 = ˇ 4 Since J>0, J= p ˇ=2More than just an online double integral solver WolframAlpha is a great tool for calculating indefinite and definite double integrals Compute volumes under surfaces, surface area and other types of twodimensional integrals using WolframAlpha's double integral calculatorInteractive graphs/plots help visualize and better understand the functions For more about how to use the Integral Calculator, go to "Help" or take a look at the examples
As argued above, the original integral will be twice as large as this integral It follows that ∫ 1 0 ∫ 1 0 emax(x2,y2)dydx= e−1 ∫ 0 1 ∫ 0 1 e max ( x 2, y 2) d y d x = e − 1Since x x is constant with respect to y y, move x x out of the integral The integral of 1 x2 y2 1 x 2 y 2 with respect to y y is 1 x arctan( y x) C 1 x arctan ( y x) C Simplify the answer Tap for more steps Combine 1 x 1 x and arctan ( y x) arctan ( y x) Simplify SimplifyIntegral of e^x^2 using the Imaginary Error Function!The "real" version https//youtube/jkytxdedxhU💪 Join our channel membership to unlock special perks,




Integral Calculator Integrate With Wolfram Alpha




Integral Of Exp X 2 Hd Version Youtube
θ is the angle of deviation of theIntegrate x^2 sin y dx dy, x=0 to 1, y=0 to pi; Integrate e^(x^2) Homework Equations The Attempt at a Solution I have no idea at all Answers and Replies #2 HallsofIvy Science Advisor Homework Helper 41,3 964 There's a reason for that That function, like most integrable functions, does not have an antiderivative that can be written in terms of elementary functions



1



What Is The Complete Solution Of Double Integration Of Dx Dy 1 X2 Y2 Quora
E 2x2 dx e y2 dy= Z 1 0 Z 1 0 e (x y2) dxdy View this as a double integral over the rst quadrant To compute it with polar coordinates, the rst quadrant is f(r;©05 BE Shapiro Page 3 This document may not be reproduced, posted or published without permission The copyright holder makes no representation about the accuracy, correctness, orFollow my work via http//JonathanDavidsNovelscomThanks for watching me work on my homework problems from my college days!




Calculate The Double Integral Iint R X Y 2 E X 2 Y 2 Dx Dy Where R Is The Square With Vertices 6 0 0 6 6 0 0 6 Study Com



Canvas Harvard Edu Courses 376 Files 9169 Download Verifier M1wmosj4bwi4u4hkdddc4nngghmnpqbpqy0kz8wt
The function mathy=e^{x^2}/math should be familiar to you It defines the normal or gaussian distribution function This is what its curve looks like There is no known function which has a derivative equal to mathe^{x^2}/math In other Evaluate ∫∫xy(x y)dxdy for x, y ∈ R over the region between y = x^2 and y = x asked in Mathematics by Nakul ( 701k points) integral calculusEvaluate the double integral of e(x^2y^2) where x = sqrt(9y^2) and the y axis Show transcribed image text Expert Answer Previous question Next question Transcribed Image Text from this Question Evaluate the given integral by changing to polar coordinates ex2y2 dA, where D is the region bounded by the semicircle x = V92 and the yaxis




Double Integration




Answered Let E X Y 2 E R 1 X 2 1 Bartleby
Triple Integrals in Spherical Coordinates The spherical coordinates of a point M (x,y,z) are defined to be the three numbers ρ,φ,θ, where ρ is the length of the radius vector to the point M;So integral of e^(x^2) dx = (e^u)*1/(2*sqrt(u))du after that i do integration by parts both ways but eventually end up with (e^u)*1/(2*sqrt(u))du = (e^u)*1/(2*sqrt(u))du sorry but i am hopeless with latex help appreciated Can do it as you would any other Can check this by differentiating the RHSAnswer to Evaluate the following integral in spherical coordinates \int \int_D \int e^{(x^2 y^2 z^2)^{3/2}}dV, D is a sphere of radius 2 By




B Tech Ii Unit 3 Material Multiple Integration



2
Example 1586 Setting up a Triple Integral in Spherical Coordinates Set up an integral for the volume of the region bounded by the cone z = √3(x2 y2) and the hemisphere z = √4 − x2 − y2 (see the figure below) Figure 15 A region bounded below by a cone and above by a hemisphere SolutionCompute integral integral_E integral x dV, where E = ( (x, y, z) x lessthanorequalto 0, z lessthanorequalto 0, x^2 y^2 z^2 lessthanorequalto 9} Sketch the solid whose volume is given by the iterated integralCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history
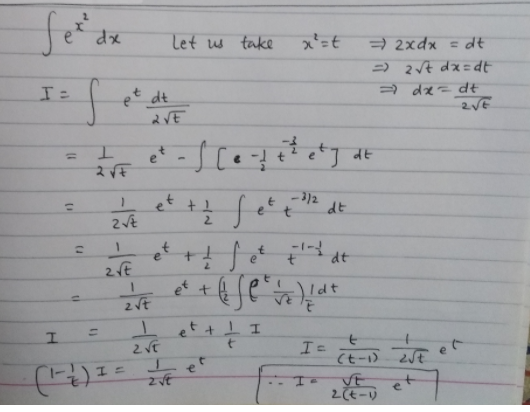



Integral E X 2 Dx Wegglab




Integration Ex 1 X2 1 2 Sin 1x 1 1 X2 1 2 Dx Explain In Great Detail Mathematics Topperlearning Com Ymrxhuvv
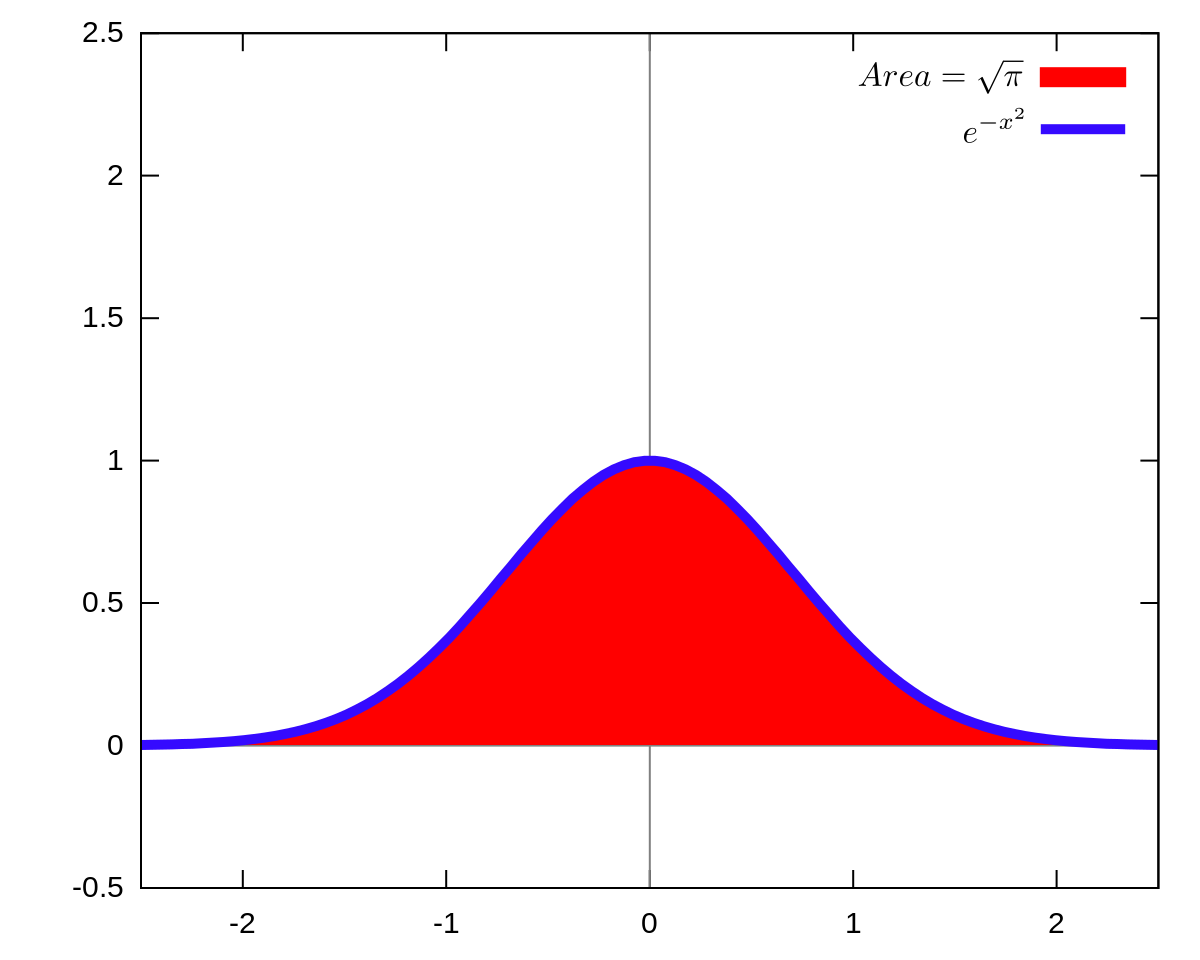
{eq}\int_0^{\sqrt 2} \int_{y^2}^2 y^3 e^{x^3}dxdy {/eq} Double Integrals When we have a double integral like the one above, where we really have no idea how to even begin to evaluate it,The Gaussian integral, also known as the Euler–Poisson integral, is the integral of the Gaussian function f = e − x 2 {\displaystyle f=e^{x^{2}}} over the entire real line Named after the German mathematician Carl Friedrich Gauss, the integral is ∫ − ∞ ∞ e − x 2 d x = π {\displaystyle \int _{\infty }^{\infty }e^{x^{2}}\,dx={\sqrt {\pi }}} Abraham de Moivre originally discovered this type of integral in 1733, while Gauss published the precise integralEvaluate integral of e^(xy) with respect to x Let Then , so Rewrite using and Tap for more steps Let Find Tap for more steps Differentiate Since is constant with respect to , the derivative of with respect to is Differentiate using the Power Rule which states that is where



Gaussian Integral Formula And Proof Semath Info




1 Point Use Spherical Coordinates To Evaluate The Triple Integral Dv E X Y Z E Vx2 Y2 Homeworklib
Hence, evaluating the triple integral using spherical coordinates yields `int int int_E e^(x^2y^2z^2)^3/2 = (4pi/3)(e1)` Approved by eNotes Editorial TeamCalculus Find the Integral e^ (2y) e2y e 2 y Let u = 2y u = 2 y Then du = 2dy d u = 2 d y, so 1 2du = dy 1 2 d u = d y Rewrite using u u and d d u u Tap for more steps Let uThis integral of a function along a curve C is often written in abbreviated form as ∫Cf(x, y)ds Example 1621 Compute ∫Cyexds where C is the line segment from (1, 2) to (4, 7) We write the line segment as a vector function r = 1, 2 t 3, 5 , 0 ≤ t ≤ 1, or in parametric form x = 1 3t, y = 2 5t Then ∫Cyexds = ∫1 0(2 5t)e1




Evaluate The Iterated Integral Integral 1 2 Chegg Com



Solved Evaluate The Given Integral By Changing To
Evaluate the double integral over the rectangular region Rdouble integration bounded region R (xy)/(sqrt(x^2y^21))dA ; T Evaluate Green's theorem using a computer algebra system to evaluate the integral \(\displaystyle \int_C xe^y\,dxe^x\,dy\), where \(C\) is the circle given by \(x^2y^2=4\) and is oriented in the counterclockwise directionIntegrate 1/(cos(x)2) from 0 to 2pi;




Integral Gausa Vikipediya



2
Homework Statement \\int{\\frac{e^x}{x^2}dx} Homework Equations Integration by substitution Integration by parts \\int{u\\ dv}=uv\\ \\ \\int{v\\ du} The Attempt at a Solution Since it was clear that integration by substitution would not work, I tried integration by parts Best Answer #1 378 5 It depends on the limits of the integration If the limits are ±infinity then the integral can be done analytically see below However, if at least one of the limits is finite then the integral can only be done numerically (an exception is if one of the limits is zero, then the integral from zero to infinity isUsing Fubini's theorem, we can convert the two onedimensional integrals into just one twodimensional integral $$ I^2 = ∫_{∞}^∞ ∫_{∞}^∞ e^{(x^2y^2)}\,dx\,dy = ∫_{ℝ^2} e^{\mathbf{z}^2}\,d\mathbf{z} $$ (we have used the formula $(x,y) = √{x^2y^2}$, which allowed us to write $e^{(x^2y^2)} = e^{(x,y)^2} = e^{\mathbf z^2}$)



Integral E T 2 Substitution Mathelounge




Calculate Particular Integral D 2 Dd 2d Prime2 Y 1 E X
Integral of integral of integral of x^2y^2z^2 \square! INTEGRAL LINKS Basic Integral Problems https//youtube/gZKoyR6ZcgIntegration by parts ∫ log x/x^2 dx https//youtube/SVGDrup8EyMINTEGRATE ∫ 1/(√9xGet stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!



2 Set Up The Definite Integral Of The Region Usi Gauthmath




Evaluation Of The Gaussian Integral Exp X 2 Cool Math Trick Youtube
Use some kind of approximation method There is no nice, finitely expressible antiderivative (Other that to write int e^(x^2) dx, of course)FOLLOW ME ON TWITTER https//twittercom/MisterMattyMoThis video shows the process for integrating e^(x^2), the Gaussian IntegralTo avoid ambiguous queries, make sure to use parentheses where necessary Here are some examples illustrating how to ask for an integral integrate x/(x1) integrate x sin(x^2) integrate x sqrt(1sqrt(x)) integrate x/(x1)^3 from 0 to infinity;




5 Double Integrals Over Rectangular Regions Pdf Free Download




Exercise 3 2 Application Of Integration In Economics And Commerce Problem Questions With Answer Solution
φ is the angle between the projection of the radius vector −− → OM on the xy plane and the x axis;Integral of exp(x^2)Instructor Christine BreinerView the complete course http//ocwmitedu/1802SCF10License Creative Commons BYNCSAMore information aExample 4 Evaluate \begin{align*} \iint_\dlr (x^2y^2)\, dx\,dy \end{align*} where $\dlr$ is the region pictured below Solution The region can be described simply if we change to coordinates $\cvarfv$ and $\cvarsv$ where \begin{align} \cvarfv &= yx\notag\\ \cvarsv&=xy \label{thechangevar} \end{align} With this change of variables, our new region of integration $\dlr^*$ is $0 \le \cvarfv



Integral Calculator With Steps




Integral Of Exp X 2 Gaussian Integral Trick Youtube
If you liked my science video, yoIf you want to integrate over both x and y, then you can convert it to an integral in polar coordinates ∫ ∞ − ∞∫ ∞ − ∞e − ( x2 y2) dx dy = ∫ ∞ 0 ∫2π 0 e − r2 r dθ dr = 2π∫ ∞ 0 e − r2 r dr = π∫ ∞ 0 e − u du Share answered Nov 9 '14 at 2231 Ross Millikan Ross Millikan 356k 26 26 gold badges



1
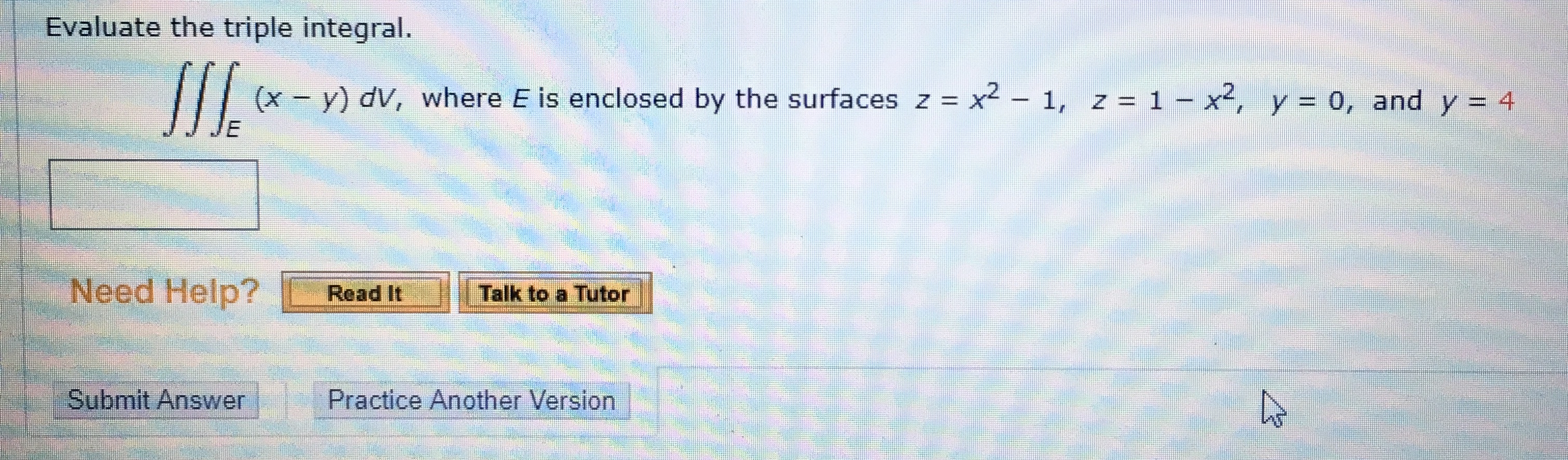



Answered Evaluate The Triple Integral X Y Bartleby




Gaussian Integral Wikipedia Republished Wiki 2




Integrating E X 2 The Gaussian Integral Youtube




Evaluate The Integral Int 3 3 Int 0 Sqrt 9 X 2 E X 2 Y 2 Dy Dx Study Com




Evaluate The Following Double Integral Over The Qu Gauthmath




Notes Up To Ch7 Sec3




Fun Sources Integral Of E X 2



Ocw Mit Edu Resources Res 18 001 Calculus Online Textbook Spring 05 Textbook Mitres 18 001 Strang 14 Pdf



Http Www Utdallas Edu Efrom Solhw Pdf




Gaussian Integral Wikipedia




Evaluate The Iterated Integral By Converting To Polar Chegg Com




Evaluate The Triple Integral E X 6y Dv E X 6y Dv Where Ee Is Bounded By The Parabolic Cylinder Y 6x2y 6x2 And The Planes Z 8x Y 12x Z 8x Y 12x And Z 0z 0 Homeworklib




The Double Improper Integral E Dy Dx May Be Defined Chegg Com




Evaluate The Double Integral Doubleintegral R Chegg Com




Verify The Given Function Including The Integral E X 2 Mathematics Stack Exchange




Use Polar Coordinates To Evaluate The Double Integral Chegg Com
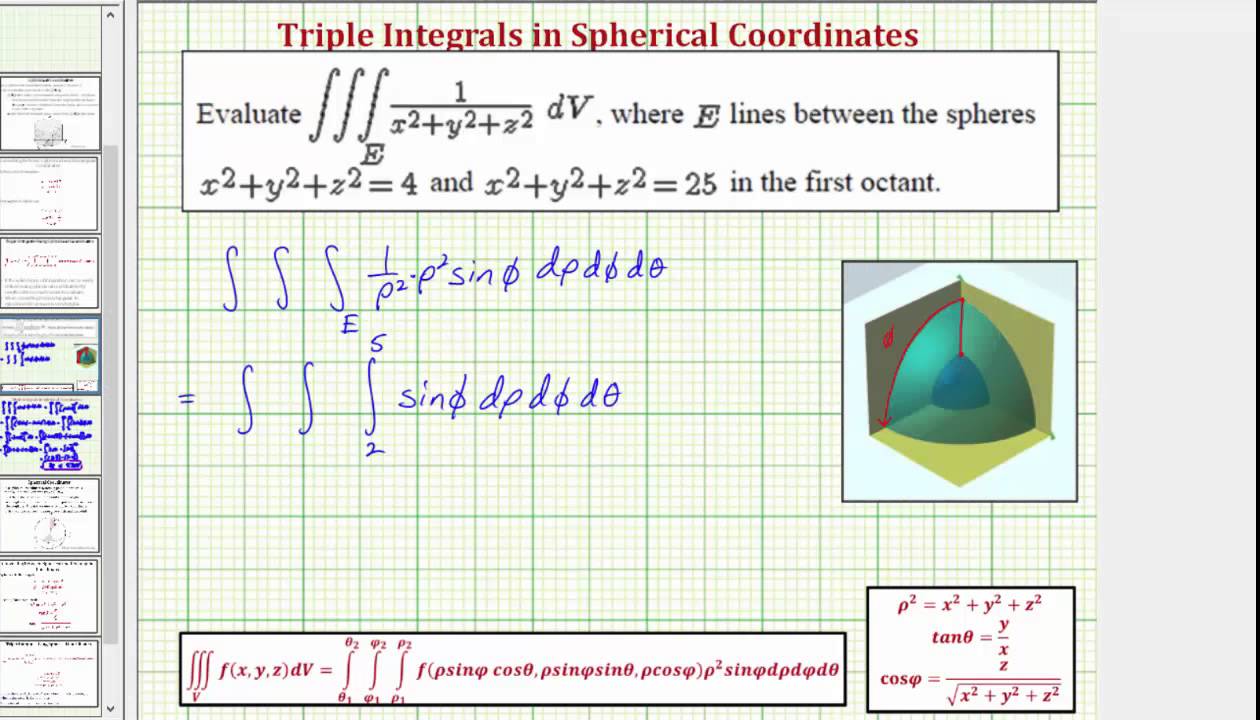



Evaluate A Triple Integral Using Spherical Coordinates Triple Integral Of 1 X 2 Y 2 Z 2 Youtube




Consider The Improper Double Integral Integral Chegg Com
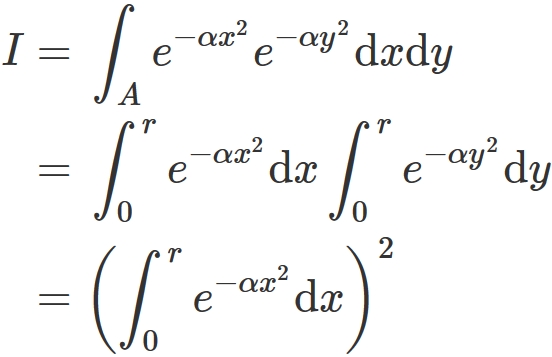



Gaussian Integral Formula And Proof Semath Info




Gaussian Integral Wikipedia



1



Gaussian Integral Wikipedia



Www3 Nd Edu Ajorza Courses 16s M550 Work 10sol Pdf



Integrate E X 2 Youtube




Calc3 1001 By James Bardo Issuu




How Do You Integrate E X 2 From 0 To 1 Socratic




Ex 7 5 6 Integrate 1 X2 X 1 2x Class 12 Ex 7 5



Integrate 2e X




B Tech Ii Unit 3 Material Multiple Integration




Se Cylindrical Coordinates To Evaluate The Triple Integral Ex2 Y2 Dv Ex2 Y2dv Where E Is Brainly Com



Double Integral Of Y 2 E X 4 Learnmathsfree Youtube



1



Canvas Harvard Edu Files Download Download Frd 1 Verifier Uicc4gewmilbskycdu7jq6cnx2jjsjmmqz2jgarh




Compute The Following Double Integrals Sketch The Chegg Com




Evaluate The Double Integral E X 2 Y 2 Da Where R Chegg Com




Answers To The Review Problems For The First Exam 251 05 10 In Spring 06




Integrating Iint D 2xy Exp Y 2 Dxdy Over The Given Region Using Polar Coordinates Mathematics Stack Exchange




Evaluate The Given Integral By Changing To Polar Coordinates Double Integral Exp X 2 Y 2 Da Where D Is The Region Bounded By The Semicircle X 4 Y 2 1 2 And The Y Axis Homework Help And Answers



Evaluating Double Integrals




Use The Change Of Variables X U 2 V 2 Y 2uv To Evaluate The Integral E Where E Is The Region Bounded By The X Axis And The Parabolas Y 2 4 4x And Y 2 4 4x




Gaussian Integral Wikipedia




We Define The Improper Integral Over The Entire Chegg Com




Double Integrate D X Y E X 2 Y 2dxdy Where D Is Chegg Com




Integral From Infinity To Infinity Of Exp X 2 Is Sqrt Pi I Always Found This Very Elegant Studying Math Mathematics Geometry Maths Algebra



Evaluate E X Y Zdzdydx For Z Y X 0 Log2 0 X 0 X Logy Sarthaks Econnect Largest Online Education Community
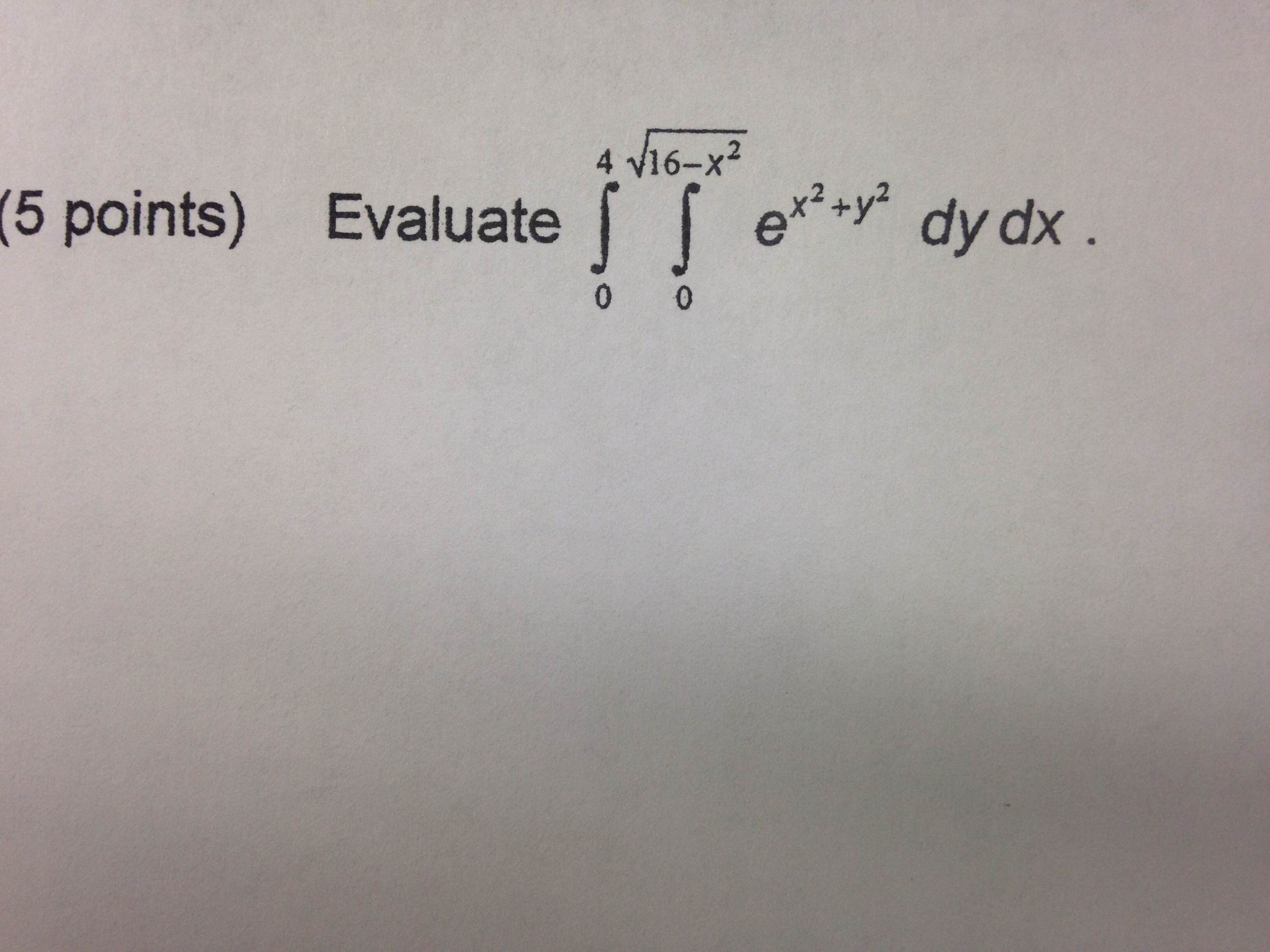



Evaluate Double Integrate E X 2 Y 2 Dydx Chegg Com




Find The Particular Integral Of D 2 3d 2 Y E 3x




Fun Sources Integral Of E X 2




Ex 4 Set Up And Evaluate A Triple Integral Of X Y 4z Youtube




Evaluate The Triple Integral 3z Dv Where E Is Bounded By The Cylinder Y 2 Z 2 9 And The Planes Study Com




Gaussian Integral Wikipedia Republished Wiki 2
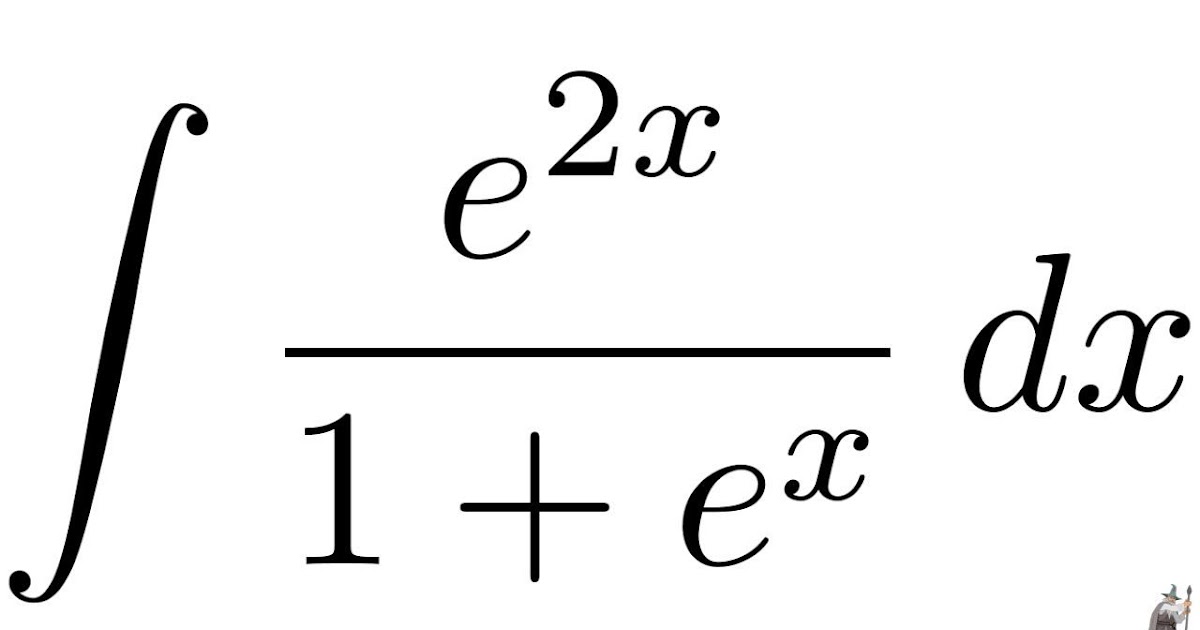



Fun Sources Integral Of E X 2




Document



Www Ualberta Ca Rjia Math215 Hwks Sol5 Pdf



What Is The Integration Of E Power Y X With Limits 0 To 2 And 0 To X Quora




Gaussian Integral Wikipedia Republished Wiki 2




Use Polar Coordinates To Evaluate The Double Integral Chegg Com
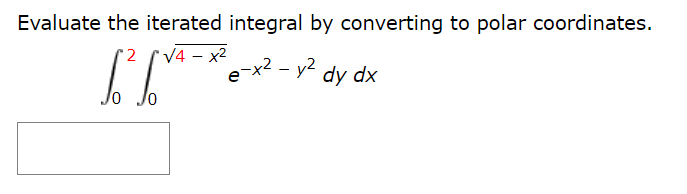



Answered Evaluate The Iterated Integral By Bartleby
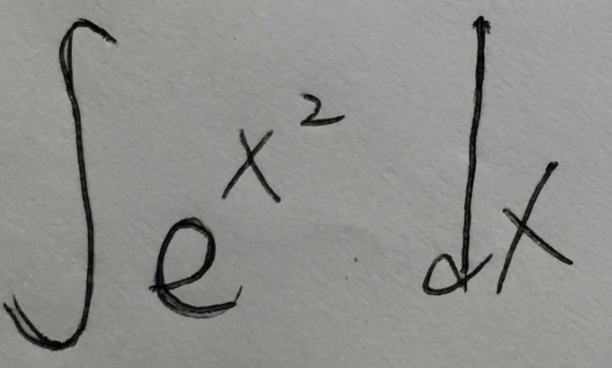



Integral E X 2 Dx Wegglab




Evaluate The Double Integral Of Exp X 2 Y 2 Where The Solid Is The Half Circle Given By X 2 Y 2 4 And X Y 0 Mathematics Stack Exchange



Http Macs Citadel Edu Zhangli Courses Taught Fall16 Courses Math231 Quiz14 Key Pdf




Final Exam 17 Questions Studocu



What Is The Particular Integral Of The Given Differential Equation D 2y Dx 2 3dy Dx 2y E E X Quora



Integral Of E X 2 Wxlasopa



Yourmathsolver The Gaussian Integral




Math Double Integrals Ppt Download



Integral Of Exp X 2 From To
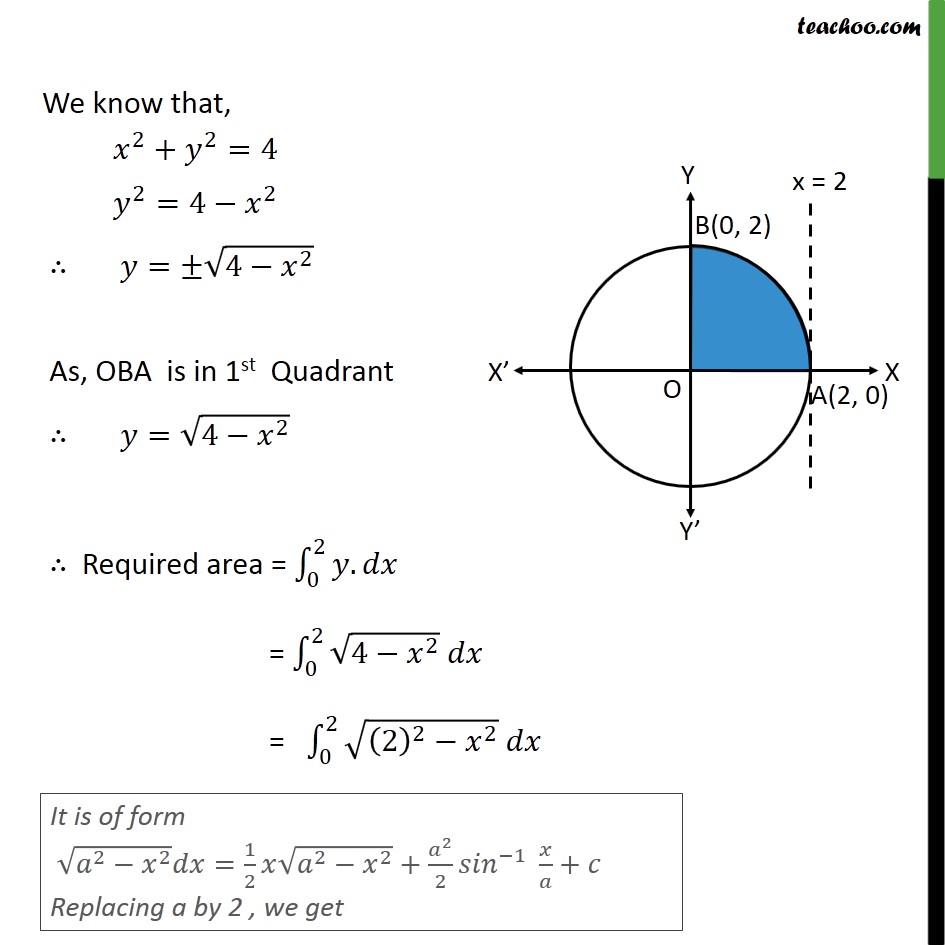



Ex 8 1 12 Area Bounded By Circle X2 Y2 4 And Lines X 0



Why Is E X 2 Non Integrable Quora



Test The Improper Integral E X2 For Convergence Stumbling Robot



2




Double Integral E X Y 2 With Outer Limits 1 And 2 And Inner Limits 0 And Y 2 Brainly In
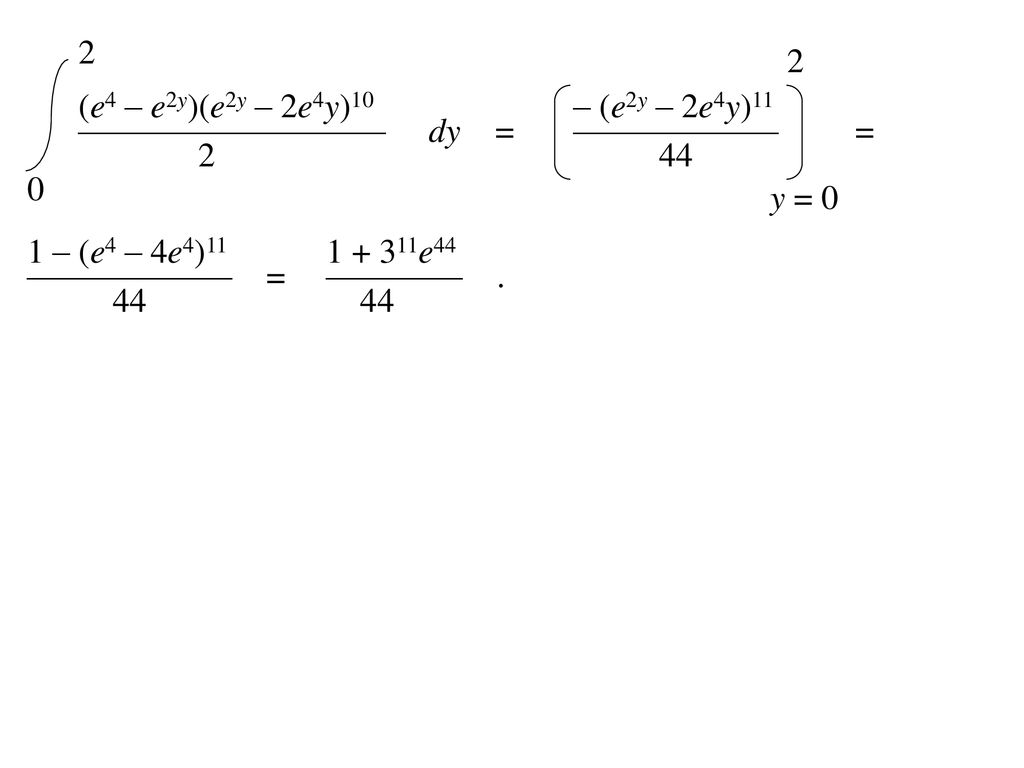



E2 Log X Example Consider The Integral X E2y 2e4y 10 Dy Dx 1 Ppt Download



Web Northeastern Edu He Wang Teaching Teachingnotes Calculus3 Handout15 6 Pdf




Evaluate The Given Integral By Changing To Polar Coordinates Double Integral E X 2 Y 2 Da Where D Is The Region That Lies To The Left Of The Y Axis Between The Circles X 2 Y 2




Solution Of Xy Dy Dx Y 3 E X 2 Is
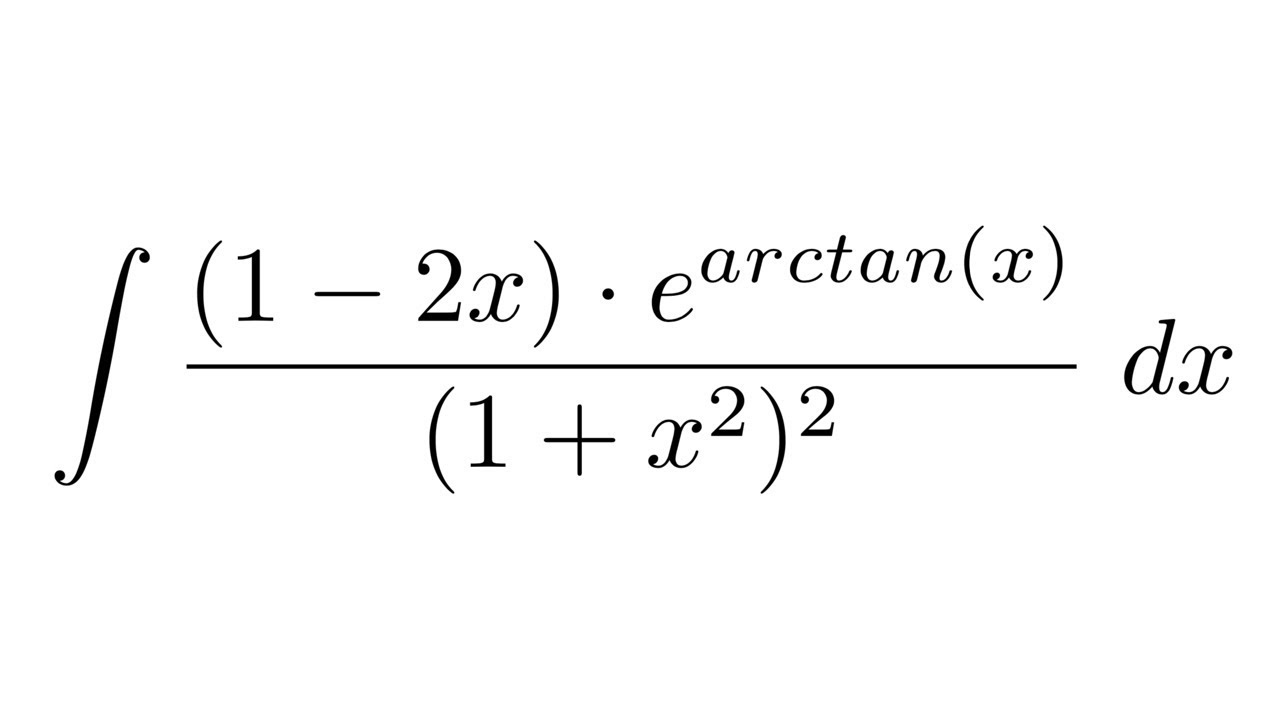



Integral Of 1 2x E Arctan X 1 X 2 2 By Parts Youtube



0 件のコメント:
コメントを投稿